I know that Lorentz force for a charge $q$, with velocity $\vec{v}$ in magnetic field $\vec{B}$ is given by
$$\vec{F} =q \vec{v} \times \vec{B}$$
but there will exist a frame of reference where observer move at same velocity with that of charge $q$, so according to him $v=0$. hence he will see no magnetic force is exerted on charge $q$. I have work on this problem for a while and found that the special relativity predicts equivalent electric force will acting upon charge instead. I want to know the relationship between this equivalent electric force and magnetic force. Thanks in advance
Answer
I haven't read them, but this, this, this and this thread (I thank a diligent Qmechanic) are related and clear up the but why-questions you might have.
The transformation of the quantities in electrodynamics with respect to boosts are
$$ \begin{alignat}{7} \mathbf{E}'&~=~ \gamma \left(\mathbf{E} + \mathbf{v} \times \mathbf{B}\right) &&+ \left(1 - \gamma\right) \frac{\mathbf{E} \cdot \mathbf{v}}{v^2} \mathbf{v} \\[5px] \mathbf{B}'&~=~\gamma\left(\mathbf{B}-\frac{1}{c^2}\mathbf{v} \times \mathbf{E}\right)&&+\left(1-\gamma\right)\frac{\mathbf{B} \cdot \mathbf{v}}{v^2} \mathbf{v} \\[5px] \mathbf{D}'&~=~ \gamma \left(\mathbf{D}+\frac{1}{c^2} \mathbf{v} \times \mathbf{H} \right) && + \left( 1 - \gamma \right) \frac{\mathbf{D} \cdot \mathbf{v}}{v^2} \\[5px] \mathbf{H}'&~=~ \gamma \left(\mathbf{H} - \mathbf{v} \times \mathbf{D}\right) && +\left(1 - \gamma\right) \frac{\mathbf{H} \cdot \mathbf{v}}{v^2}\mathbf{v} \\[5px] \mathbf{j}' & ~=~ \mathbf{j} - \gamma \rho \mathbf{v} && + \left(\gamma - 1 \right) \frac{\mathbf{j} \cdot \mathbf{v}}{v^2} \mathbf{v} \\[5px] \mathbf{\rho}' & ~=~ \gamma \left(\rho - \frac{1}{c^2} \mathbf{j} \cdot \mathbf{v}\right) \end{alignat} $$where $\gamma \left(v \right)$ and the derivation of the transformation is presented on this Wikipedia page and is most transparent in a space-time geometrical picture, see for example here. Namely, the electromagnetic field strength tensor $F_{\mu\nu}$ incorporates both electric and magnetic field $E,B$ and the transformation is the canonical one of a tensor and therefore not as all over the place as the six lines posted above.
In the non-relativistic limit $v For the traditional force law, the first formula confirms the prediction that the new $E$ magnitude is $vB$. Also, beware and always write down the full Lorentz law when doing transformations. Lastly, I'm not sure if special relativity predicts equivalent electric force will acting upon charge instead is the right formulation you should use, because while the relation is convincingly natural in a special relativistic formulation, the statement itself is more a consistency requirement for the theory of electrodynamics. I'd almost say the argument goes in the other direction: The terrible transformation law of $E$ and $B$ with respect to Galilean transformations was known before 1905 and upgrading the status of the Maxwell equations to be form invariant when translating between inertial frames suggests that the Lorentz transformation (and then special relativity as a whole) is physically sensible.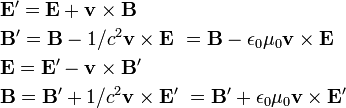
No comments:
Post a Comment