Adrian Puzzlinger has gone missing again. Even worse, for puzzle lovers, the latest puzzle under construction is missing as well. The puzzle police are puzzled by an imprint of aligned lists of numbers on a notepad on the desk in the puzzler parlor of Adrian Puzzlinger.
$$\small \boxed{ \begin{matrix} \\[-9mu] & & & 3 & 6 & 10 & 15 & 21 & 28 & 36 & \\[7mu] & & & 4 & 7 & 11 & 16 & 22 & 29 & 37 & \\[7mu] & & & 16 & 23 & 29 & 34 & 38 & 41 & 43 & \\[7mu] & & & 17 & 24 & 30 & 35 & 39 & 42 & 44 & \\[7mu] & 36 & 37 & 38 & 39 & 40 & 41 & 42 & 43 & 44 & \\[-9mu] \\ \end{matrix} } $$
What kind of puzzle was Adrian making?
As this kind of puzzle has assumed different aliases, the authorities need a full description of how Adrian used these lists, not just a name.
Other missing-puzzler case
The mess of Adrian Puzzlinger
Answer
The puzzle is:
Kakuro $ \small\sf \kern6em example \! : $
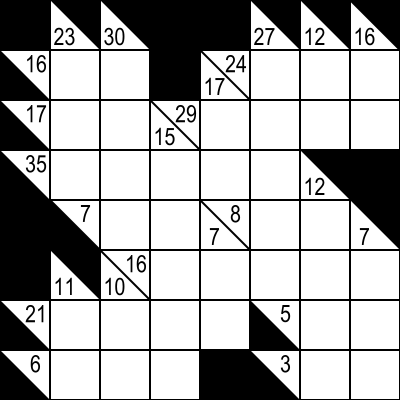
because:
The numbers in the top row represent the minimum sum of a run of length n. min(2) =3, min(3) = 6 etc. Basically the triangle numbers. The numbers in the 4th row are the maximum sum of a run of length n. Row 2 is just one bigger than row 1, and row 3 is one less than row 4. Thus rows 1 to 4 represent all the sums that can appear in a run for which all elements are known. For example if the sum of a run of length 2 is 4, then you know the numbers must be 1 and 3. if the sum was 3, it must be 1 and 2. If the sum was 17, it must be 9 and 8, and if 16 it must be 7 and 9. This is true because you can't have the same number appearing twice in any row, so e.g. 4=2+2 is not allowed. Any other sum than those shown would permits multiple possible sets. E.g. a sum of 6 could be either 1,5 or 2,4. The last row is all possible sums of a run of length 8 for which all elements are known. for example 44 can only be 2,3,4,5,6,7,8,9. It seems that all possible sums with a unique set of elements are shown.
Edit:
actually the unique sum for a run of 9 is not shown (45). Maybe he was doing a kakuro problem which didn't have any 9-runs.
Annotated lists:
$$ \require{begingroup} \begingroup \def \S{\kern25.8mu} \small \begin{matrix} \sf \kern68mu 2 \S 3 \S 4 \S 5 \S 6 \S 7 \S 8 \\ \boxed{ \begin{matrix} \\[-9mu] & & & 3 & 6 & 10 & 15 & 21 & 28 & 36 & \\[-3mu] & & & 4 & 7 & 11 & 16 & 22 & 29 & 37 & \\[7mu] & & & 16 & 23 & 29 & 34 & 38 & 41 & 43 & \\[-3mu] & & & 17 & 24 & 30 & 35 & 39 & 42 & 44 & \\[7mu] & 36 & 37 & 38 & 39 & 40 & 41 & 42 & 43 & 44 & \\[-9mu] \\ \end{matrix} } \\ \kern2mu \sf 9 \S 8 \S 7 \S 6 \S 5 \S 4 \S 3 \S 2 \S 1 \end{matrix} ~~~~ \begin{array}{l} l ~=~ \textsf{row length} \\[19mu] \textsf{sum:} ~~~ 1 ~~~ 2 ~~\, \cdots ~~ (l{-}1) ~~~ l \\[-4mu] \textsf{sum:} ~~~ 1 ~\!\; (2) ~ \cdots ~~ (l{-}1) ~~~~~~ (l{+}1) \\[7mu] \textsf{sum:} ~~~ 9 ~\!\: (8) \; \cdots ~~ (m{+}2) ~~~~~~~~~~ m \\[-4mu] \textsf{sum:} ~~~ 9 ~~~ 8 ~~\, \cdots ~~ (m{+}2) ~~ (m{+}1) \\[6mu] \textsf{sum:} ~~ \textsf{all but } m, ~~~ \textsf{row length} = 8 \\[19mu] m ~= \unicode{8220}\textsf{missing}\unicode{8221} =~ 9-l \end{array} \endgroup $$

No comments:
Post a Comment