homework and exercises - Solving the two body problem numerically

I'm trying to solve the two body problem numerically, setting up $G$, $m1$ and $m2$ to be equal to 1. then I located each mass on positions -5 and 5 respectively along the $x$ axis and gave them both 0 on the $y$ axis. I'm having trouble finding the initial conditions fitting for circular movement. Please help!

Answer

For common center (barycenter) orbits, the velocities will be \begin{align} v_1&=\sqrt{\frac{Gm_2r_2}{\left(r_1+r_2\right)^2}}\\ v_2&=\sqrt{\frac{Gm_1r_1}{\left(r_1+r_2\right)^2}} \end{align} which, since $m_1=m_2$ and $r_1=r_2$, will be the same value, $v\approx0.22$ for your values of $G,\,m,\,r$. Since you've placed the two objects along the $x$ axis, then you need to give them this velocity in the $\pm y$ direction and 0 in the $x$ direction (the positive/negative value being associated with the direction of motion of the particle).

You can see why with the below diagram from the Wikipedia entry on circular motion,

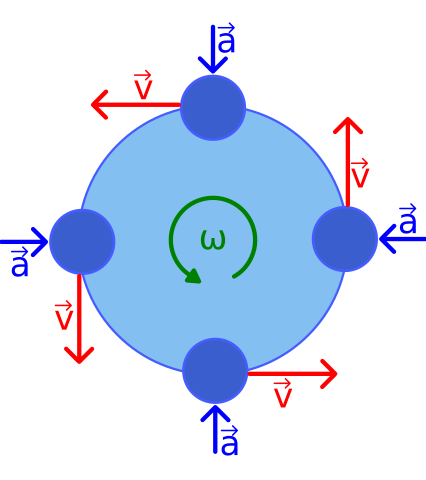
At any one of the four cardinal points, the velocity is purely in the tangential direction. For example, consider the top point; it is at $(x,y)=(0,1)$ with a velocity of $(v_x,\,v_y)=(-v,0)$. You can do the same analysis with the other 3 points. So rather than trying to determine a random $(x,y)$ point, you can simply use the cardinal points to set the positions and velocities.